S15-01 算法-数组、栈
[TOC]
基础
概述
在前面的课程中我不断的强调一个编程的真相:编程的最终目的只有一个:对数据进行操作和处理。
- 评判编程能力、水平的高低,要看你是否可以更好的操作和处理数据。
- 在之前的很多课程中,我经常和同学们强调一个事实:所有的编程(无论是前端、后端、算法、人工智能、区块链,也不论 是什么语言 JavaScript、Java、C++等等)最终的目的都是为了处理数据。
当你拿到这些数据时,以什么样的方式存储和处理会更加方便、高效,也是评判一个开发人员能力的重要指标(甚至是唯一的指标)。
虽然目前很多的系统、框架已经给我们提供了足够多好用的 API,对于大多数时候我们只需要调用这些 API 即可。
但是如何更好的组织数据和代码,以及当数据变得复杂时,以什么方式处理这些数据依然非常重要。
只有可以更好的处理数据,你才是一个真正的开发工程师,而不只是一个 API 调用程序员。
以前端、后端为例:
前端从后端获取数据,对数据进行处理、展示;
和用户进行交互产生新的数据,传递给后端,后端进行处理、保存到数据库,以便后续读取、操作、展示等等;
数据结构与算法的本质:
数据结构与算法的本质就是一门专门研究数据如何组织、存储和操作的科目。
算法+数据结构=程序(Algorithm+Data Structures=Programs)
数据结构与算法事实上是程序的核心,是我们编写的所有程序的灵魂。
只有掌握了扎实的数据结构与算法,我们才能更好的理解编程,编写扎实、高效的程序。
包括对于程序的理解不再停留于表面,甚至在学习其他的系统或者编程语言时,也可以做到高屋建瓴、势如破竹。
应用
无论是操作系统(Windows、Mac OS)本身,还是我们所使用的编程语言(JavaScript、Java、C++、Python 等等),还是 我们在平时应用程序中用到的框架(Vue、React、Spring、Flask 等等),它们的底层实现到处都是数据结构与算法,所以你 要想学习一些底层的知识或者某一个框架的源码(比如 Vue、React 的源码)是必须要掌握数据结构与算法的。
以前端为例:框架中大量使用到了栈结构、队列结构等来解决问题(比如之前看框架源码时经常看到这些数据结构,Vue 源码、 React 源码、Webpack 源码中可以看到队列、栈结构、树结构等等,Webpack 中还可以看到很多 Graph 图结构);
实现语言或者引擎本身也需要大量的数据结构:哈希表结构、队列结构(微任务队列、宏任务队列),前端无处不在的数据 结构:DOM Tree(树结构)、AST(抽象语法树)。
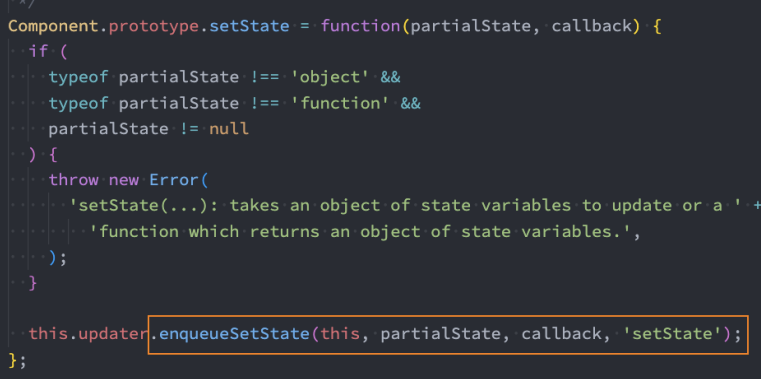
Vue 源码中的数据结构:
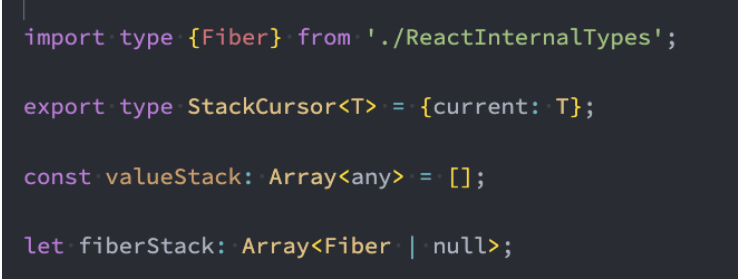
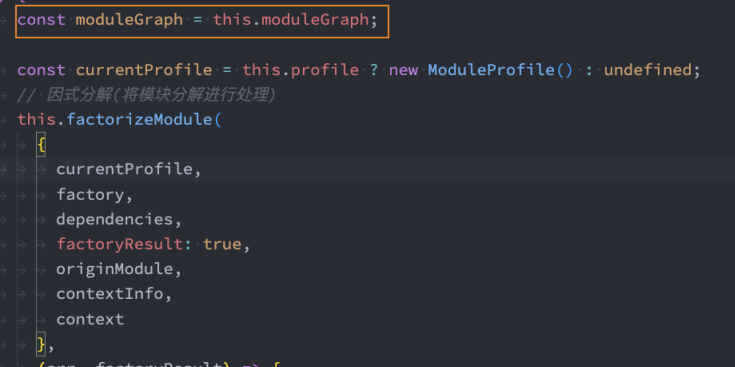
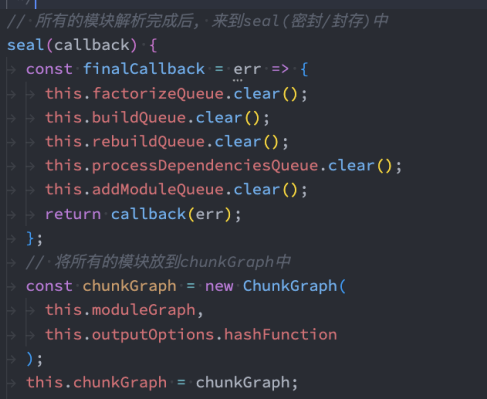
React、Webpack 源码中的数据结构:
面试要求
互联网大厂、高级岗位面试都会要求 必须要掌握一定的数据结构与算法:
因为对于很多企业来说,想要短时间考察一个人的能力以及未来的潜力,数据结构与算法是非常重要指标,也会成为它们的硬性条件。
- 对于可以将数据结构与算法掌握很好的开发人员来说,通常对于业务的把握肯定是没有问题的。
- 并且对于系统的设计也会更加合理,可以写出更加高效的代码。
对于想要进入大厂的同学,经常会刷leetcode:
- 但是对于大多数同学来说,leetcode 上的题目晦涩难懂,代码无从下手,不会解题。
- 只有系统的掌握了数据结构与算法,才能将这些题目融会贯通,面试遇到相关的题目就可以对答如流。
逻辑思维、代码能力提升离不开对于数据的处理:
- 我们已经强调了所有的编程最终的目的都是为了处理数据。
- 而数据结构与算法就是一门专为讲解数据应该如何存储、组织、操作的课程。
- 所以学习数据结构与算法可以更好的锻炼我们的逻辑思维能力和代码编程能力,帮助我们平时在处理一些复杂数据时,可以更好的编 写代码,写出更高效的程序。
并且掌握数据结构与算法后,如果想要转向其他的领域(比如从前端转到后端、算法工程师等)也会更加容易:
- 因为所有的编程思想都是相通的,只是换了一种语言来处理数据而已。
- 对于未来更多的领域,比如人工智能、区块链,数据结构与算法也是它们的基石,是必须要掌握的一门课程。
学习方法
数据结构与算法通常被认为 晦涩难懂、复杂抽象,对于大多数人来说学习起来是比较困难的。
那么通常学习数据结构与算法有哪些方式呢?
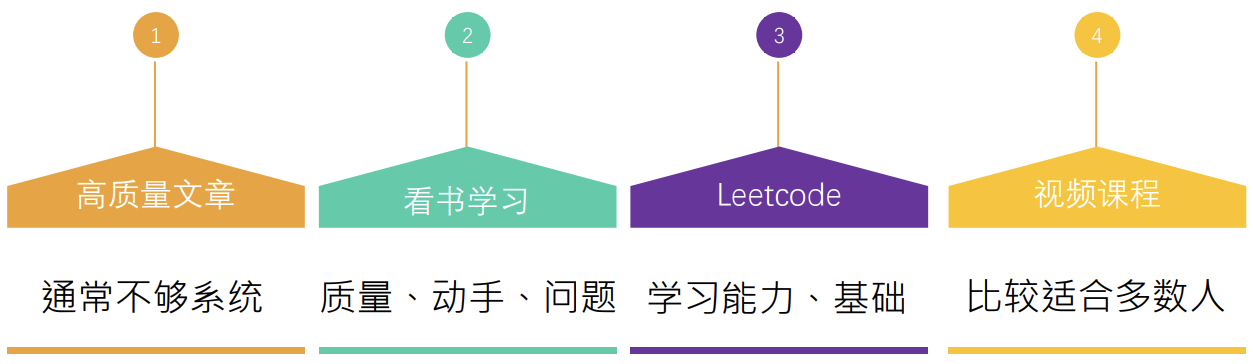
TS 常见数据结构与算法
数据结构
概念
数据结构(Data Structure): 数据结构是计算机中用于组织和存储数据的方式。它涉及到如何将数据以及相互之间的关系组织起来,以便能够高效地访问和处理数据。常见的数据结构有数组、链表、栈、队列、树、图等。
常见数据结构

在计算机中对于数据的组织和存储结构也会影响我们的效率。
性能:
- 常见的数据结构较多每一种都有其对应的应用场景,不同的数据结构 的 不同操作 性能是不同的。
- 有的查询性能很快,有的插入速度很快,有的是插入头和尾速度很快。
- 有的做范围查找很快,有的允许元素重复,有的不允许重复等等。
- 在开发中如何选择,要根据具体的需求来选择。
跨语言:
注意: 数据结构和语言无关,常见的编程语言都有 直接或者间接 的使用上述常见的数据结构
应用场景:
为什么之前学习 JavaScript 没有接触过数据结构呢? 好像只见过数组。
- 这是因为很多数据结构是需要在进行高阶开发(比如设计框架源码)时才会用到的。
- 甚至某些数据结构在 JavaScript 中本身是没有的,我们需要从零去实现的。
你可能会想:老师,我觉得不多呀,赶紧给我们讲讲怎么用的就行了。
- 我们不是要讲这些数据结构如何用,用是 API 程序员的思考方式,我们要讲的是这些数据结构如何实现,再如何使用。
- 了解真相,你才能获得真正的自由。
算法
算法(Algorithm): 算法是解决问题的一种方法或步骤。常见的算法包括排序算法(如冒泡排序、快速排序、归并排序等)、查找算法(如顺序查找、二分查找等)、图形算法(如最短路径算法、最小生成树算法等)等等。
效率:
在之前的学习中,我们可能学习过几种排序算法,并且知道不同的算法,执行效率是不一样的。
解决问题的过程中,不仅仅数据的存储方式会影响效率,算法的优劣也会影响着效率。
数据结构的实现,离不开算法。
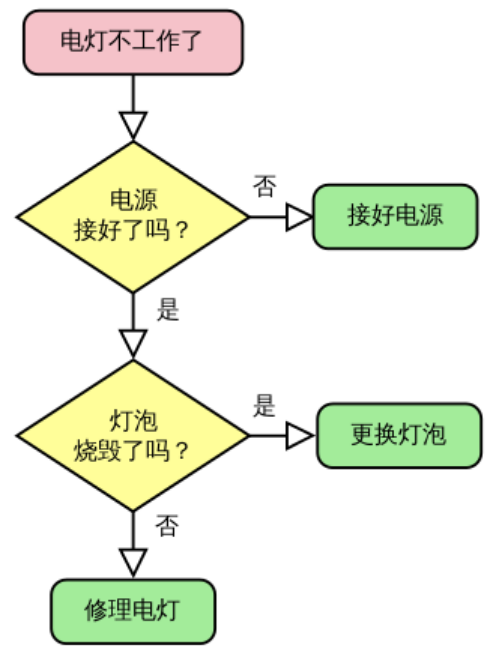
举例: 电灯不工作的解决算法
线性结构
线性结构(Linear List): 由 n(n≥0)个数据元素(节点,a[0],a[1],a[2]…,a[n-1])组成的有限序列。
其中:
- 数据元素的个数 n 定义为表的长度 = “list”.length() (“list”.length() = 0(表里没有一个元素)时称为空表)。
- 将非空的线性表(n>=1)记作:(a[0],a[1],a[2],…,a[n-1])。
- 数据元素 a[i](0≤i≤n-1)只是个抽象符号,其具体含义在不同情况下可以不同。
上面是维基百科对于线性结构的定义,有一点点抽象,其实我们只需要记住几个常见的线性结构即可

数组结构 Array
数组(Array): 是一种线性数据结构,其将相同类型的元素存储在连续的内存空间中。我们将元素在数组中的位置称为该元素的索引(index)。
▸ 数组(Array)结构是一种重要的数据结构。几乎是每种编程语言都会提供的一种原生数据结构(语言自带的)。并且我们可以借助于数组结构来实现其他的数据结构,比如栈(Stack)、队列(Queue)、堆(Heap);
▸ 数组的主要概念和存储方式:
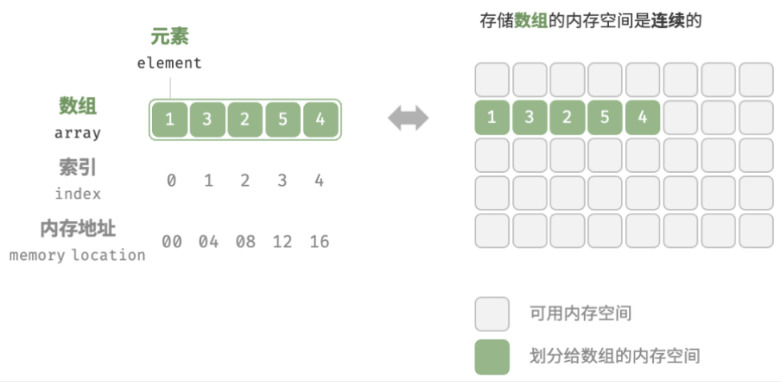
▸ 通常数组的内存是连续的,所以数组在知道下标值的情况下,访问效率是非常高的
这里我们不再详细讲解 TypeScript 中数组的各种用法,和 JavaScript 是一致的
https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Array
后续我们在讨论数组和链表的关系区别时,还会通过大 O 表示法来分析数组操作元素的时间复杂度问题。
栈 Stack
栈(Stack): 是一种遵循先入后出逻辑的线性数据结构。
我们可以将栈类比为桌面上的一摞盘子,如果想取出底部的盘子,则需要先将上面的盘子依次移走。我们将盘子替换为各种类型的元素(如整数、字符、对象等),就得到了栈这种数据结构。
▸ 我们把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。将把元素添加到栈顶的操作叫作“入栈”,删除栈顶元素的操作叫作“出栈”。
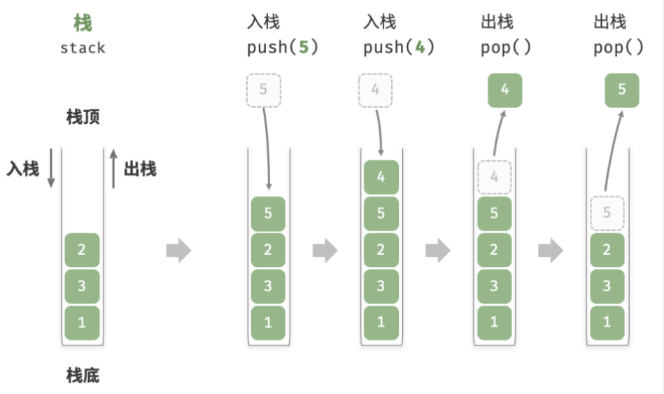
API
- push():
(el),O(1),添加一个新元素到栈顶位置。- el:
any,栈中的元素。
- el:
- pop():
(),O(1),移除栈顶的元素,同时返回被移除的元素。 - peek():
(),O(1),返回栈顶的元素,不修改栈。 - isEmpty():
(),判断栈是否为空。 - size():
(),返回栈中元素的个数。
▸ 通常情况下,我们可以直接使用编程语言内置的栈类。然而,某些语言可能没有专门提供栈类,这时我们可以将该语言的“数组”或“链表”当作栈来使用,并在程序逻辑上忽略与栈无关的操作。
/* 初始化栈 */
// TypeScript 没有内置的栈类,可以把 Array 当作栈来使用
const stack: number[] = []
/* 元素入栈 */
stack.push(1)
stack.push(3)
stack.push(2)
stack.push(5)
stack.push(4)
/* 访问栈顶元素 */
const peek = stack[stack.length - 1]
/* 元素出栈 */
const pop = stack.pop()
/* 获取栈的长度 */
const size = stack.length
/* 判断是否为空 */
const is_empty = stack.length === 0栈的实现
思路: 栈遵循先入后出的原则,因此我们只能在栈顶添加或删除元素。然而,数组和链表都可以在任意位置添加和删除元素,因此栈可以视为一种受限制的数组或链表。换句话说,我们可以“屏蔽”数组或链表的部分无关操作,使其对外表现的逻辑符合栈的特性。
数组实现
思路: 使用数组实现栈时,我们可以将数组的尾部作为栈顶。入栈与出栈操作分别对应在数组尾部添加元素与删除元素,时间复杂度都为 O(1) 。
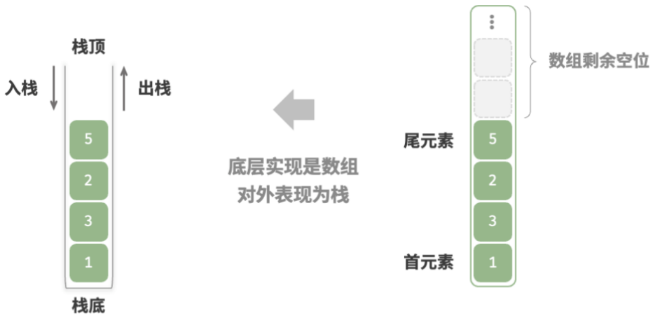
由于入栈的元素可能会源源不断地增加,因此我们可以使用动态数组,这样就无须自行处理数组扩容问题。
/* 基于数组实现的栈 */
class ArrayStack<T = any> {
// 定义一个数组,用于存储元素。注意:必须是private属性
private stack: T[] = [];
/* 获取栈的长度 */
size(): number {
+ return this.stack.length;
}
/* 判断栈是否为空 */
isEmpty(): boolean {
+ return this.stack.length === 0;
}
/* 入栈 */
push(el: T): void {
+ this.stack.push(el);
}
/* 出栈 */
pop(): T | undefined {
+ if (this.isEmpty()) throw new Error('栈为空');
+ return this.stack.pop();
}
/* 访问栈顶元素 */
peek(): T | undefined {
++ if (this.isEmpty()) throw new Error('栈为空');
return this.stack[this.stack.length - 1];
}
/* 返回 Array */
toArray() {
return this.stack;
}
}
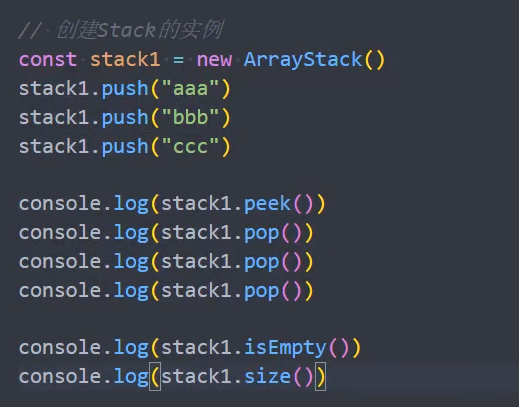
const stack1 = new ArrayStack<string>()
const stack2 = new ArrayStack<number>()测试
链表实现
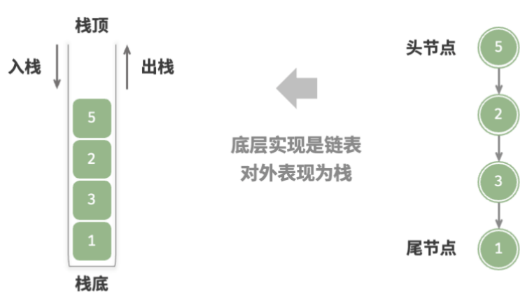
使用链表实现栈时,我们可以将链表的头节点视为栈顶,尾节点视为栈底。
对于入栈操作,我们只需将元素插入链表头部,这种节点插入方法被称为“头插法”。而对于出栈操作,只需将头节点从链表中删除即可。
以下是基于链表实现栈的示例代码:
/* 基于链表实现的栈 */
class LinkedListStack {
private stackPeek: ListNode | null; // 将头节点作为栈顶
private stkSize: number = 0; // 栈的长度
constructor() {
this.stackPeek = null;
}
/* 获取栈的长度 */
get size(): number {
return this.stkSize;
}
/* 判断栈是否为空 */
isEmpty(): boolean {
return this.size === 0;
}
/* 入栈 */
push(num: number): void {
const node = new ListNode(num);
node.next = this.stackPeek;
this.stackPeek = node;
this.stkSize++;
}
/* 出栈 */
pop(): number {
const num = this.peek();
if (!this.stackPeek) throw new Error('栈为空');
this.stackPeek = this.stackPeek.next;
this.stkSize--;
return num;
}
/* 访问栈顶元素 */
peek(): number {
if (!this.stackPeek) throw new Error('栈为空');
return this.stackPeek.val;
}
/* 将链表转化为 Array 并返回 */
toArray(): number[] {
let node = this.stackPeek;
const res = new Array<number>(this.size);
for (let i = res.length - 1; i >= 0; i--) {
res[i] = node!.val;
node = node!.next;
}
return res;
}
}抽象栈的接口
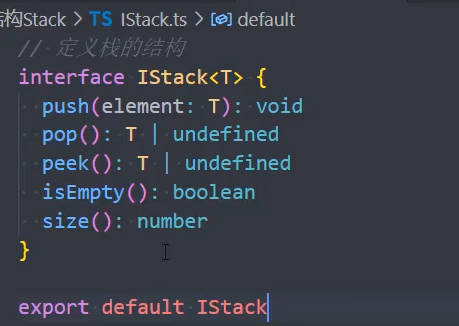
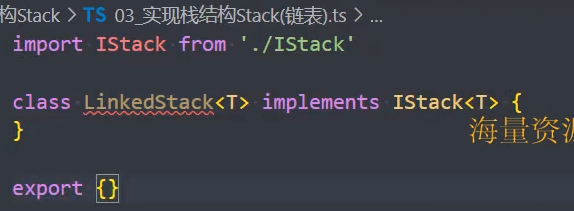
1、定义栈的接口 IStack
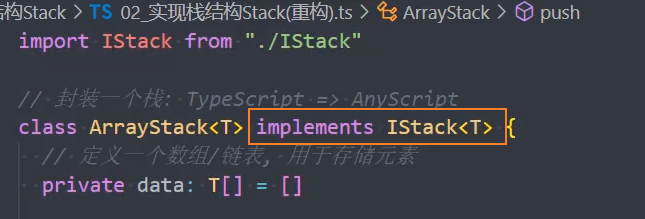
2、ArrayStack 实现栈接口
3、LinkedStack 实现栈接口
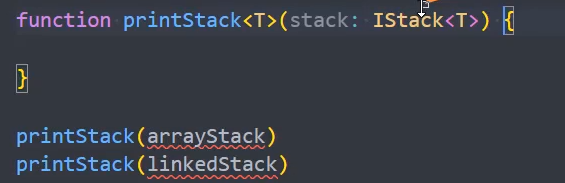
4、抽象接口是多态的基础
面试题
入栈、出栈顺序


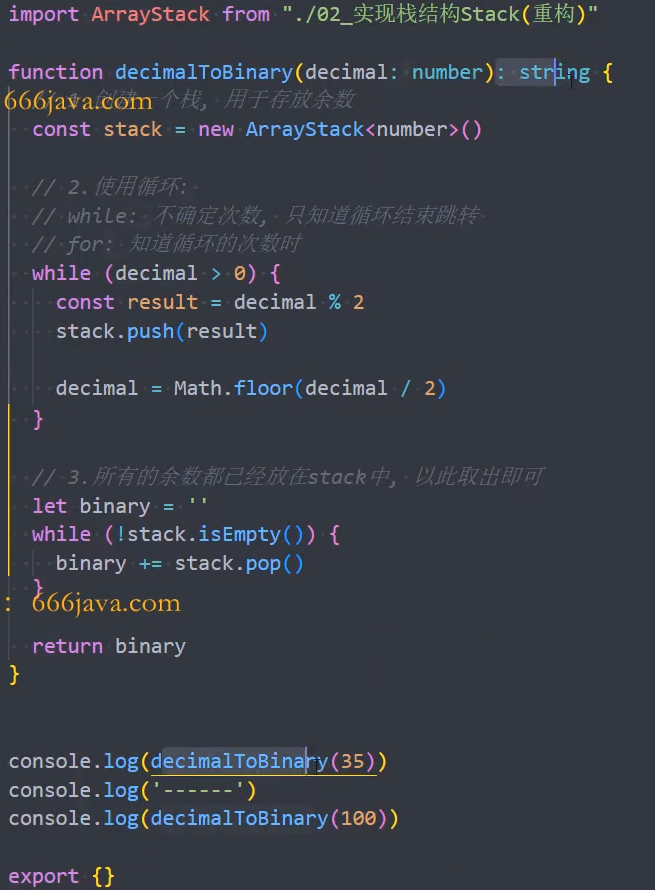
十进制转二进制
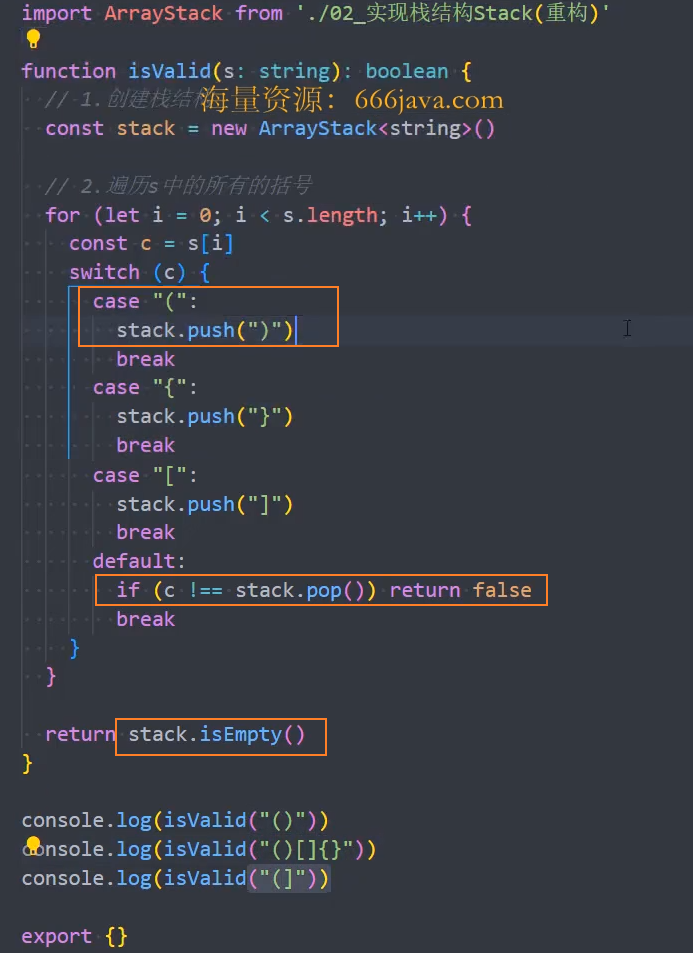
有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true示例 2:
输入:s = "()[]{}"
输出:true示例 3:
输入:s = "(]"
输出:false提示:
1 <= s.length <=10^4s仅由括号'()[]{}'组成